DIP_review_2_1 - Frequency Domain Filtering(1)

1.Fourier Transform formula

Four types of Fourier Transform
- 时域非周期时域周期
  
  频域非周期 CTFT(时间频域均连续) FS(CT,频域离散，时域连续)
  
  频域周期 DTFT(时间离散，频域连续) DFT(DT,时间频域均离散)
  - FS(CT) => $x(t) = \sum_{k=-\infty}^{\infty}a_ke^{jkw_0t}$ $x (t) = \sum_{k = - \infty}^{\infty} a_{k} e^{j k w_{0} t}$ 频率离散且无周期
    - $a_k = \frac{1}{T}\int_T x(t)e^{-jkw_0t}$ 时间连续且周期
  - CTFT => $X(jw) = \int_{-\infty}^{\infty}x(t)e^{-jwt}dt$ $X (j w) = \int_{- \infty}^{\infty} x (t) e^{- j w t} d t$ 时间连续且非周期
    - $x(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}X(jw)e^{jwt}dw$ 频率连续且非周期
  - DTFT => $X(e^{jw}) = \sum_{k=-\infty}^{\infty}x[n]e^{-jwn}, w \in [0, 2\pi], w = \frac{2\pi}{T}$ $X (e^{j w}) = \sum_{k = - \infty}^{\infty} x [n] e^{- j w n}, w \in [0, 2 π], w = \frac{2 π}{T}$ 时间离散且非周期
    - $x[n] = \frac{1}{2\pi}\int_{2\pi}X(e^{jw})e^{jwn}dw$ 频率连续且周期
  - DFT(数字图像处理，实际上也就是DT) => $X[K] =\sum_{n=<N >}x[n]e^{-jk(\frac{2\pi}{N})n} = a_k$ $X [K] = \sum_{n = < N >} x [n] e^{- j k (\frac{2 π}{N}) n} = a_{k}$
    - FS(DT\IDFT) => $x[n] =\frac{1}{N} \sum_{k=<N>}a_ke^{jk(\frac{2\pi}{N})n}$
    - DT 与 IDFT， DFT 与 DT求取a_k, 二者本质相同！！！
2D DFT and IDFT
- DFT $F(u,v) = \sum_{x= <M>}\sum_{y= <N>}f(x,y)e^{-j2\pi(\frac{ux}{M}+\frac{vy}{N})} = F_x\{F_y\{f(x,y)\}\}$
- IDFT $f(x,y) = \frac{1}{MN} \sum_{u= <M>}\sum_{v= <N>}F(u,v)e^{j2\pi(\frac{ux}{M}+\frac{vy}{N})}$
- basis function => $\frac{ux}{M}+\frac{vy}{N}$ !!!
Related calculation: 2D DFT in polar form: $F(u,v) = \| F(u,v)\|e^{-j\Phi(u,v)}$ $F (u, v) = ∥ F (u, v) ∥ e^{- j Φ (u, v)}$
- Fourier spectrum(频谱):
  - $\| F(u,v)\| = [R^2(u,v) + I^2(u,v)]^{\frac{1}{2}}$
  - 反映不同frequency的幅度
- Phase angle(相角):
  - $\Phi(u,v) = arctan(\frac{I(u,v)}{R(u,v)})$
  - 反映空间位置信息，对于图片来说相角信息比频谱信息更加重要，所以对图片处理时，我们要注意对相角的偏移和影响
- Power spectrum(功率谱)：
  - $P(u,v) = \| F(u,v)\|^2$
  - 总能量
- DC component(直流分量):
  - $F(0,0) = \sum_{x= <M>}\sum_{y= <N>}f(x,y) = MN \overline{f(x,y)}$
  - 反应图片的整体平均亮度，对于图片的亮度影响较大
- 物体轮廓在低频，特征在高频

	时域非周期	时域周期
频域非周期	CTFT(时间频域均连续)	FS(CT,频域离散，时域连续)
频域周期	DTFT(时间离散，频域连续)	DFT(DT,时间频域均离散)

2.Sampling

1D sampling
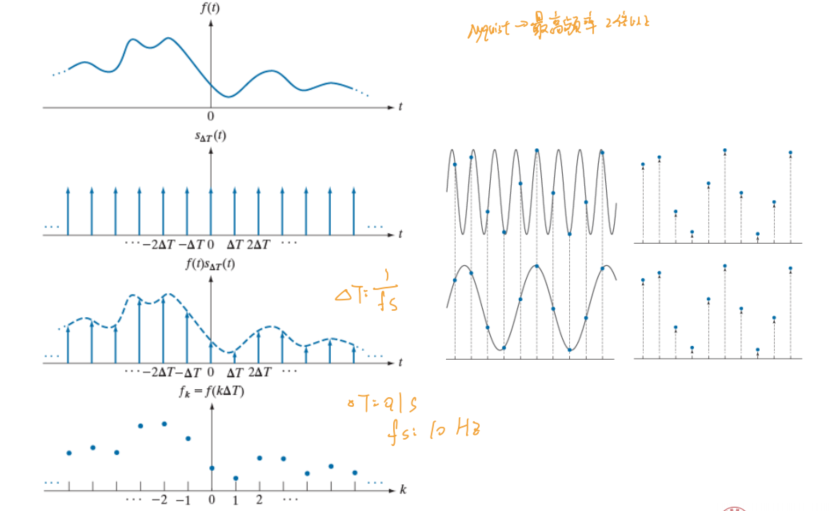
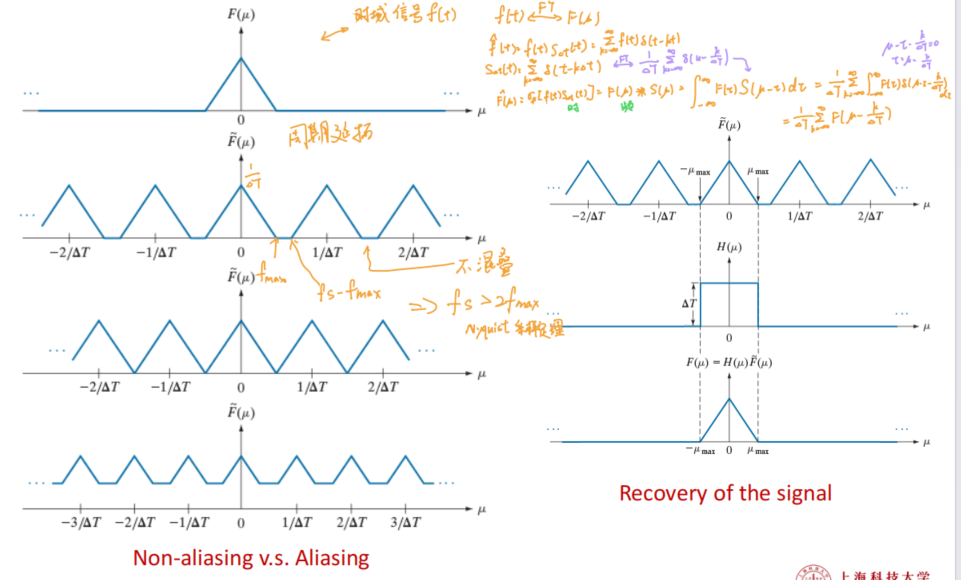
- 存在 Aliasing problem 当 $\frac{1}{\Delta T}=f_s<= 2f_{max}$
- 采样信号 $S_{\Delta T(t)} = \sum_{k=-\infty}^{\infty}\delta(t-k\Delta T) 时间\\ => S(\mu) = \frac{1}{\Delta T}\sum_{k=-\infty}^{\infty}\delta(\mu-\frac{k}{\Delta T})$ 频率
- $\hat{f(t)} = f(t)\cdot S_{\Delta T(t) = \sum_{k=-\infty}^{\infty}f(t)\delta(t-k\Delta T)}$ 采样变成周期性延拓
- $\hat{F(\mu)} = \frac{1}{\Delta T}F(\mu) * S(\mu) = \frac{1}{\Delta T}\int_{-\infty}^{\infty}F(\tau)S(\mu - \tau)d\tau \\= \frac{1}{\Delta T}\sum_{k=-\infty}^{\infty}\int_{-\infty}^{\infty}F(\tau)\delta(\mu-\tau-\frac{k}{\Delta T}) d\tau \\ = \frac{1}{\Delta T}\sum_{k=-\infty}^{\infty}F(\mu - \frac{k}{\Delta T})$ 时域转为频域卷积，同时结果表现为频率域也出现周期性延拓
2D sampling
- 采样信号 $S_{\Delta T \Delta Z}(t,z) = \sum_{m=-\infty}^{\infty} \sum_{n=-\infty}^{\infty}\delta(t-m\Delta T, z - n\Delta Z)$

3.Fourier Transform property

Translation
- $f(x,y)e^{j2\pi(\frac{u_0x}{M} + \frac{v_0y}{N})}\Leftrightarrow F(u-u_0,v-v_0)$
- $f(x-x_0,y-y_0)\Leftrightarrow F(u,v)e^{-j2\pi(\frac{u_0x}{M} + \frac{v_0y}{N})}$
- 同时可以通过频域平移简化FFTshift的操作当 $u_0 = \frac{M}{2}, v_0 = \frac{N}{2}$
Periodicity
- $f(x,y) = f(x+k_1M,y) = f(x+k_1M,y+k_2N) = f(x,y+k_2N)$
- $F(u,v) = f(u+k_1M,v) = f(u+k_1M,v+k_2N) = f(u,v+k_2N)$
- 可以参考matlab 镜像填充选择circular参数时效果
Rotation(极坐标)
- $f(r, \theta + \theta_0) \Leftrightarrow F(w,\phi+\theta_0)$

Symmetry(注意数字信号为 $[0,1,2,3,\cdots,M-1]$ 所以在 $\frac{M}{2}$ 的基础上判断对称性)

	以 $(0,0)$ 对称	以 $(\frac{M}{2},\frac{N}{2})$ 对称
偶函数even	$w(x,y) = w(-x,-y)$	$w(x,y) = w(M-x,N-y)$
奇函数odd	$w(x,y) = -w(-x,-y)$	$w(x,y) = -w(M-x,N-y)$
共轭对称(f(x,y)real)	$F^*(u,v) = F(-u,-v)$	$F^*(u,v) = F(M-u,N-v)$
共轭反对称 (f(x,y)imaginary)	$F^*(u,v) = -F(-u,-v)$	$F^*(u,v) = -F(M-u,N-v)$