DIP_review_2_1 - Frequency Domain Filtering(2)

Discrete Convolution Theorem

Convolution theorem
- $𝑓(𝑥, 𝑦) ★ ℎ(𝑥, 𝑦) ⟺ 𝐹(𝑢, 𝑣) 𝐻(𝑢, 𝑣)$
- $𝑓(𝑥, 𝑦) ℎ(𝑥, 𝑦) ⟺ \frac{1}{MN}𝐹(𝑢, 𝑣) ★ 𝐻(𝑢, 𝑣)$
Wraparound problem
- 数字信号在时域为周期信号，会产生周期性延拓，因此卷积会存在循环卷积的问题，并非得到线性卷积
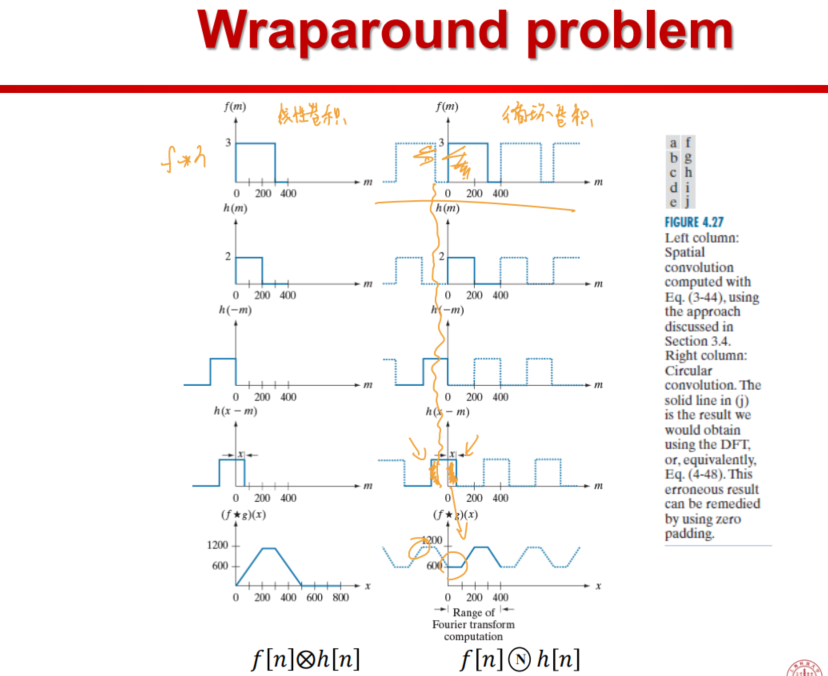
- - 线性卷积(Linear convolution)
    - $𝑓(𝑛) ⨂ ℎ(𝑛)$
  - 循环卷积
    - 当 $L<M+N-1$ ,循环卷积是线性卷积长度为L的混叠
    - 当 $L=M+N-1$ ,循环卷积=线性卷积
    - 当 $L>M+N-1$ ,循环卷积是线性卷积末尾补L-(N+M-1)个零
  - 周期卷积
    - $𝑓(𝑛)\ N\ h(n)$
    - 周期卷积是线性卷积以一定序列长度(L)为周期的周期延拓
    - 对周期卷积取主值序列得到循环卷积
- 利用zero padding来人为的改变周期，最终使得线性卷积等于循环卷积得到的结果

Frequency domain filtering

Introduction
- Basic Filtering form: $g(𝒙, 𝒚)= F^{−𝟏}[𝑯(𝒖, 𝒗)𝑭(𝒖,𝒗)]$
- 一般选择中心为 $(\frac{D}{2},\frac{Q}{2})$ ，而并非 $(0,0)$
- 一般也会进行padding后再进行卷积处理
- Steps for frequency domain filtering
  - 1. 给定input image $f(x,y)$ , 大小 $M*N$ ,进而得到padding的参数P = 2M, Q = 2N
  - 1. padding得到 $f_p(x,y)$
  - 1. Implement FFTshift, by multiplying $(-1)^{x+y}$ to center the transform(负数置为0)
  - 1. Compute the DFT 得到 $F(u,v)$
  - 1. 生成一个实对称过滤器*, $H(u,v)$ , 大小为 $P*Q$ 且中心为 $(\frac{P}{2},\frac{Q}{2})$ (padding + fftshift + DFT)
  - 1. $G(u,v) = H(u,v)F(u,v)$ , using array multiplication(vector operation)
  - 1. $g_p(x,y) = \{real[F^{-1}[G(u,v)]]\}(-1)^{x+y}$
  - 1. cut off padding region to get final result $g(x,y)$ with size of $M*N$
- 在频率域上设计滤波器eg.
Typical Lowpass filtering: 提高 $D_0$ 截止频率，使得滤波得到的图像更加清晰
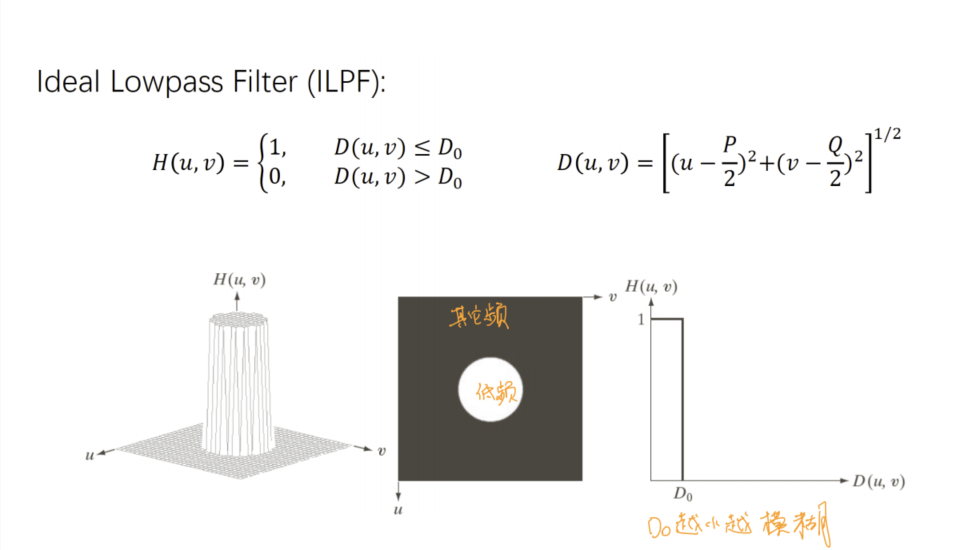
- Ideal Lowpass filter
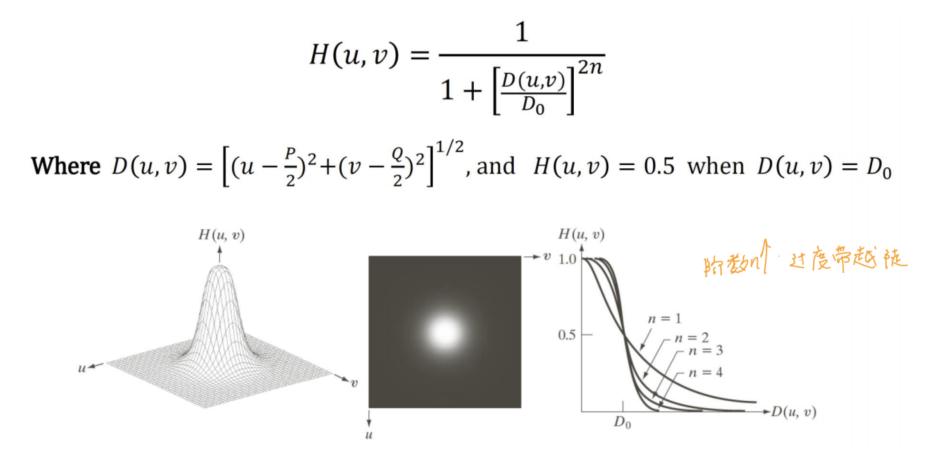
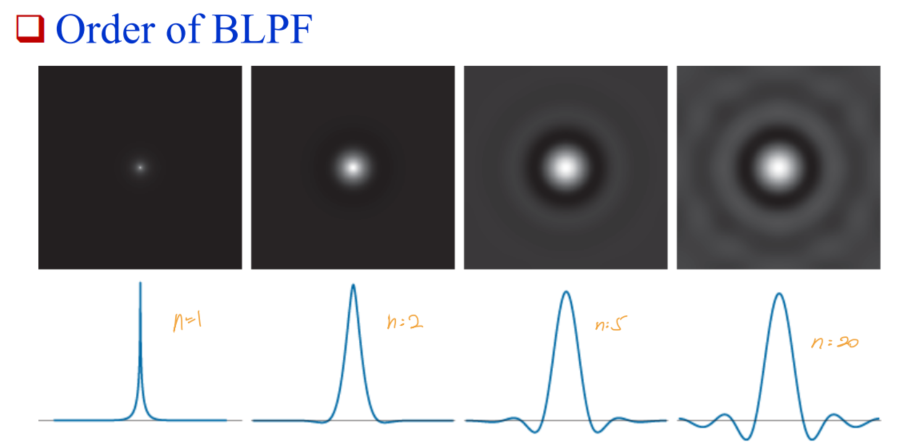
- Butterworth Lowpass filter
- Gaussian Lowpass filter
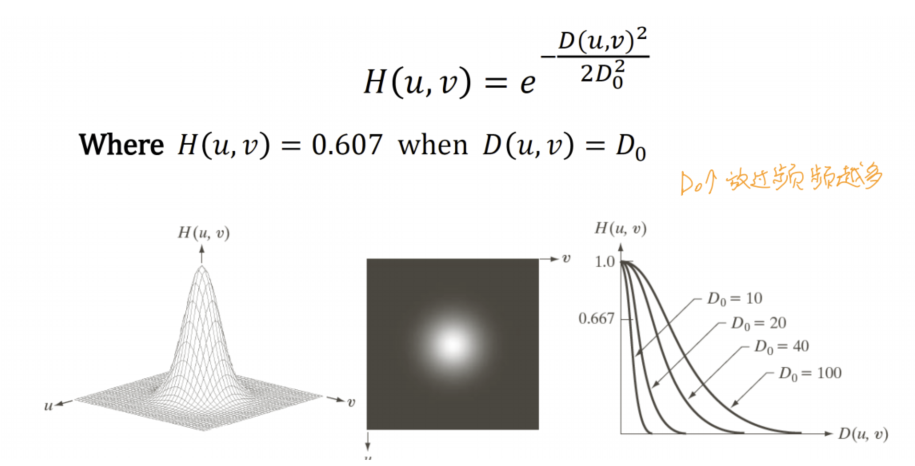
  - 现实应用场景: ps, 低通滤波除去皱纹，通过模糊来使图像更光滑，达到磨皮效果
Typical Highpass filtering: $H_{HP}(u,v) = 1 - H_{LP}(u,v)$ : 提高 $D_0$ ,会滤走更多的能量
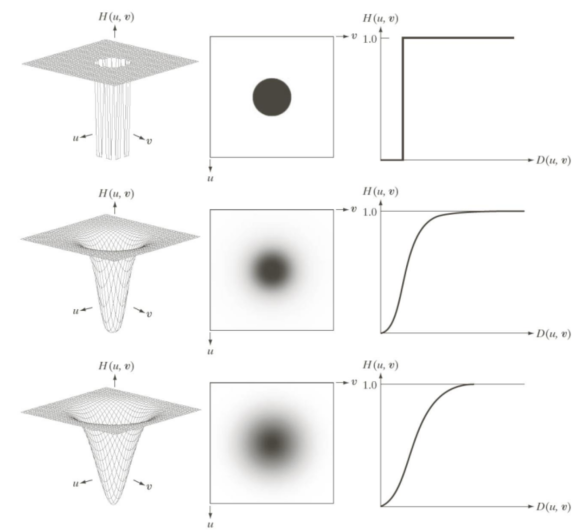
Other filtering
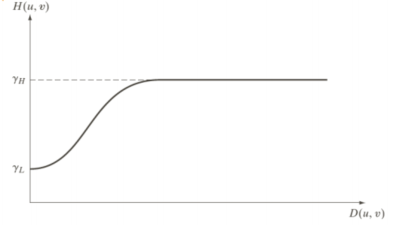
- 同态滤波(Homomorphic Filtering)
  - $f(x,y) = i(x,y)r(x,y)$ , 其中 i 表示光照, r表示达到位置对光的反射能力
  - $ln \rightarrow z(x,y) = lnf(x,y) = lni(x,y)+lnr(x,y) \\ DFT \rightarrow Z(u,v) = F_i(u,v)(low\ frequency) + F_r(u,v)(high\ frequency) \\ HPF + IDFT \rightarrow s(x,y) = F^{-1}[H(u,v)Z(u,v)] = F^{-1}[H(u,v)F_i(u,v)] + F^{-1}[H(u,v)F_r(u,v)] \\ Exp \rightarrow g(x,y) = e^{s(x,y)} = i_0(x,y)r_0(x,y)$
  - 基于高斯的HPF: $H(u,v) = (\gamma_H - \gamma_L)[1 - e^{-c[\frac{D(u,v)}{D_0}]^2}]+ \gamma_L$ $H (u, v) = (γ_{H} - γ_{L}) [1 - e^{- c [\frac{D ( u , v )}{D _{0}}]^{2}}] + γ_{L}$ ，前半部分的系数来定义滤波器高频成分的放过系数
  - 最终保留反射的高频成分
  - 适用场景：光照不均匀 or 光照变化缓慢
  - 优势：使得照明更加均匀 and 增加阴影的对比度
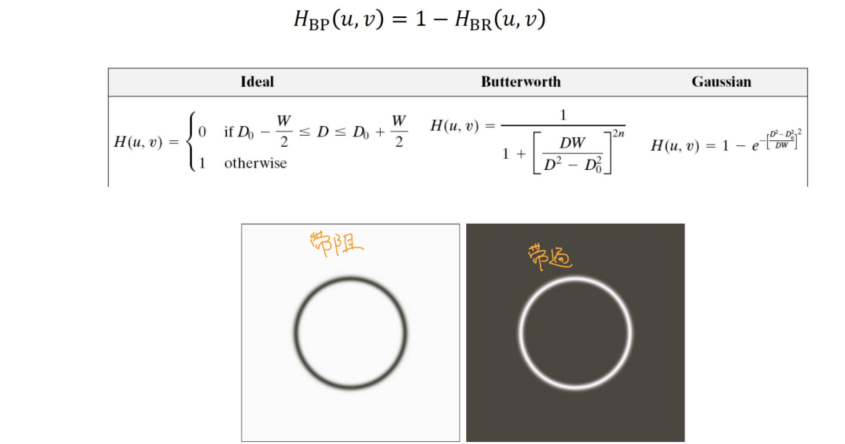
- 选择滤波(selective filtering)
  - 带通(bandpass filter)
  - 带阻(bandreject filter)
  - 陷波器(Notch filter)
    - 最佳陷波滤波器