Deconvolution
Deconvolution
- Torch Function
- torch.nn.ConvTranspose2d()
- 经常出现在需要进行上采样的地方,通俗来讲,就是需要进行特征恢复或者图像扩大的地方。而之所以称其为“逆卷积”,是因为该方法进行上采样的方式与卷积操作互为“逆过程”。但也仅限于区域恢复,而无法确定原来的特征值在卷积域内的分布情况。
- 参数列表
- in_channels (int) – Number of channels in the input image
- out_channels (int) – Number of channels produced by the convolution
- kernel_size (int or tuple) – Size of the convolving kernel
- output_padding (int or tuple, optional) – Additional size added to one side of each dimension in the output shape. Default: 0
- stride (int or tuple, optional) – Stride of the convolution. Default: 1
- 此处的stride与卷积不同,相当于对中间输入,进行区域扩张插值,而并非卷积核的跨度!!!
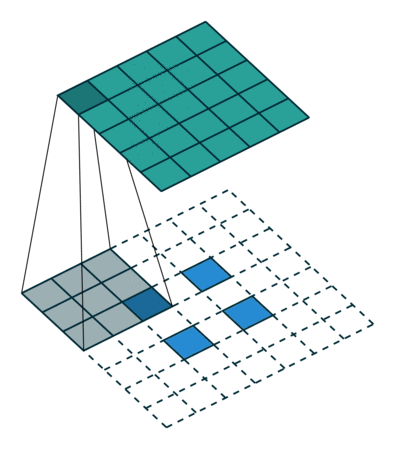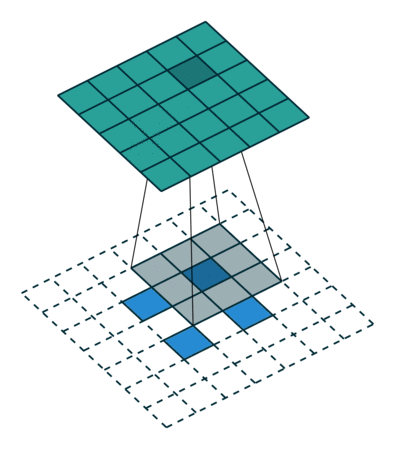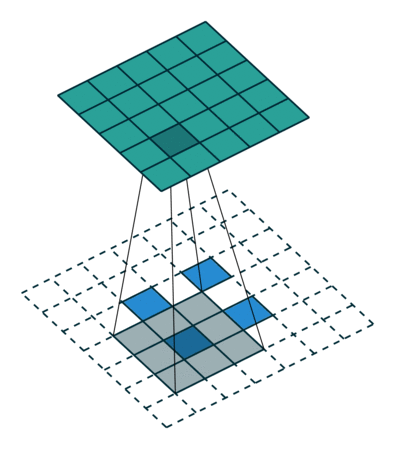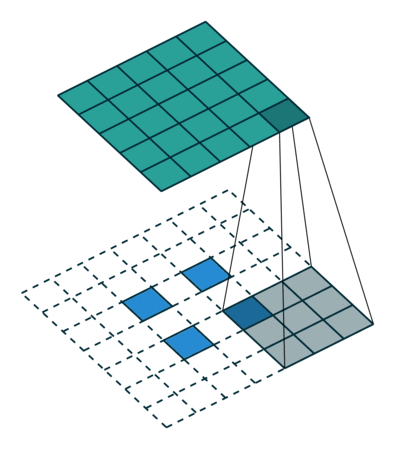
- padding (int or tuple, optional) – dilation * (kernel_size - 1) - padding zero-padding will be added to both sides of each dimension in the input. Default: 0
- 此处的padding也与卷积不同,注意deconv的核心是 “恢复” 即最终得到的图像要等于卷积前的
m,因此在最原始的情况 no padding 时,注意针对的是卷积时no padding的情况,逆卷积扩展(k-1)!!!!才可以保证最终的输出结果可以为m - Conv :
- Deconv :
- 此处的padding也与卷积不同,注意deconv的核心是 “恢复” 即最终得到的图像要等于卷积前的
- Detail derivation
- basic formula
- 加入 stride
s中间图像扩张插值- Conv :
- 对做
k-1扩展,并且插值扩张,每组pixel之间插入个,一共有组 - Deconv :
- 加入 padding
p原始图像填充- Conv :
- 对此时不用做
k-1扩展,而为k-1-p扩展 - Deconv :
- 同时加入stride
s和 paddingp - Conv :
k-1-p扩展, 并且插值扩张,每组pixel之间插入个,一共有组- Deconv :
- Final formula
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.









