DIP_review_2_4
DIP_review_2_4 - Wavelet and Other Image Transforms
1 Unitary transform 酉变换(找到合适的基函数(完备正交基)去压缩数据,且满足能量守恒定律)
- 前向变换
- 逆向变换
- 酉变换需要满足的条件为
A的逆矩阵等于其共轭对称矩阵 - eg1. 图像旋转矩阵
- eg2. PCA参数矩阵
- eg3. DFT傅里叶变换
- 2D unitary transform

2. Frequency Domain Extension
2.1 DCT离散余弦变换
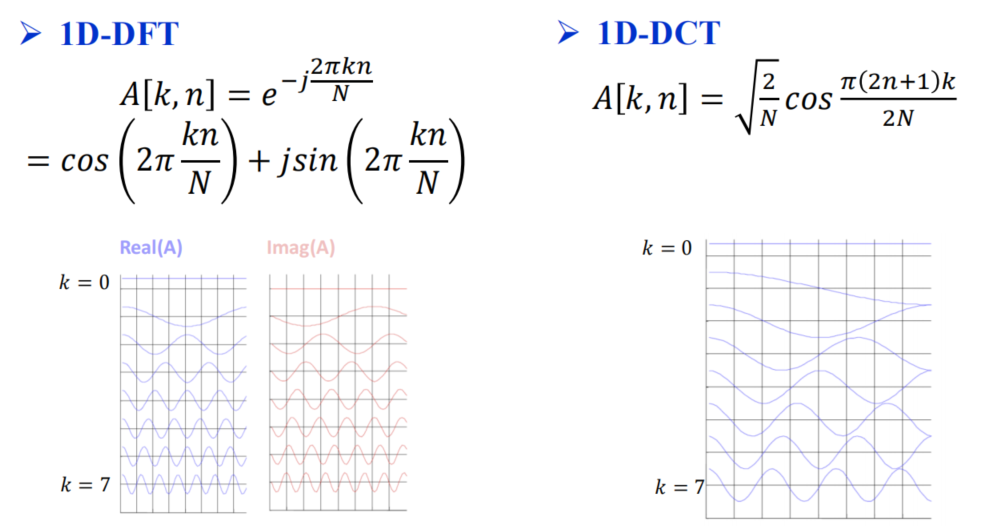
- ad
- 实数
- 频率更小,与相同DFT相差两倍
- 能够有效的对数据进行压缩,只在重要的频率域上系数有所聚集
- 也能进行快速变换
2.2 Walsh Transform
- 由±1组成的棋盘图案,每一行均为basis function
- forward
- Inverse
- Hadamard Matrix Ordering(不满足,差系数,所以能量发生改变;但能以简单的系数可表示图像)
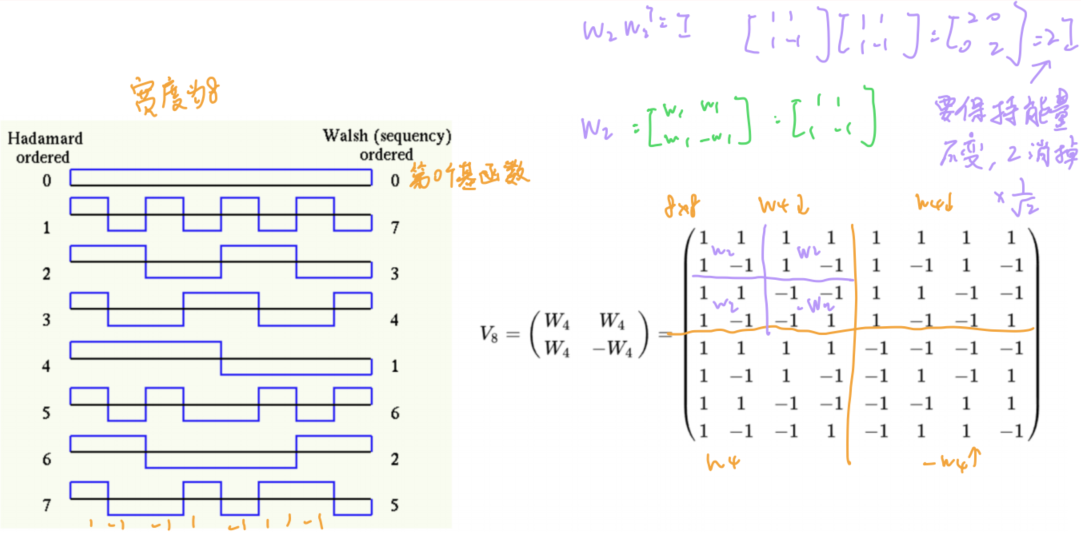
2.3 Discrete Wavelet Transform (DWT)
- 为了描述某一可变“时间”内的频率的变化,傅里叶可进行带窗变换,但太宽或太窄均会影响最终的展示效果,因此提出了小波(有限振荡)变换,通过平移
translate和scale缩放母小波来实现!!! - Harr transform matrix

AVE得到低频成分,并且可逆可继续拆分DIFF得到高频成分
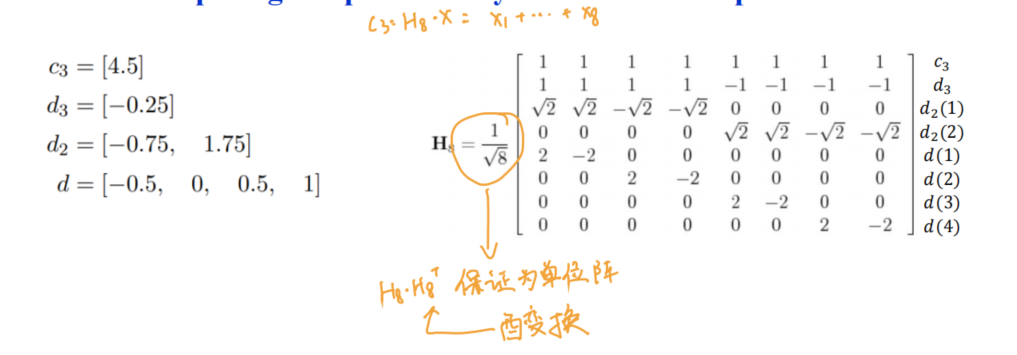
- 因此只需要最basic的的低频和全部高频我们就可以复原原信号

- 其中
H1就可以作为母小波通过对其做平移和尺度变换就可以得到其他小波
- 其中
- Mother wavelet母小波
- 能量有限
- 不改变信号本身自带的能量
- 1D-DWT

- 2D-DWT

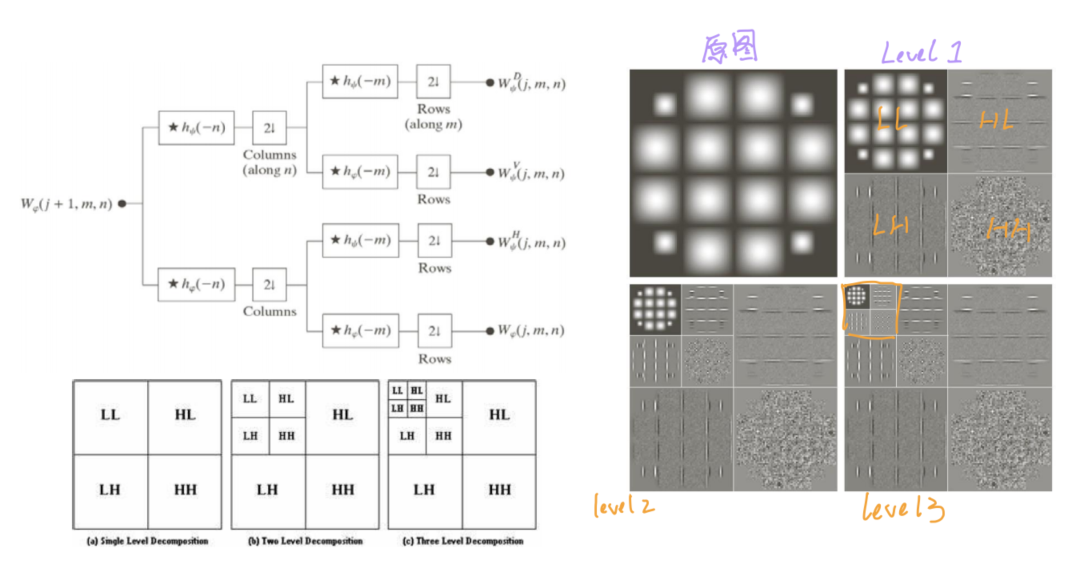
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.











