CV_learning_notes(6)
Fitting
Least Squares 最小二乘法
- Assumption:仅考虑真实值与预测值之间的误差, 计算的是 与 之间的距离
- Formula:
- Solution:
- 但是如果line是vertical,最小二乘法将会失效
Total Least Squares 总体最小二乘法
- Assumption: 同时考虑因变量和自变量中的误差,使用直线表示法,可处理vertical case,计算的是 到直线 的垂直距离
- Formula:
-
Solution:
- 由 可得
- 将 代入可得化简形式
- 最终对 求解可最终解得
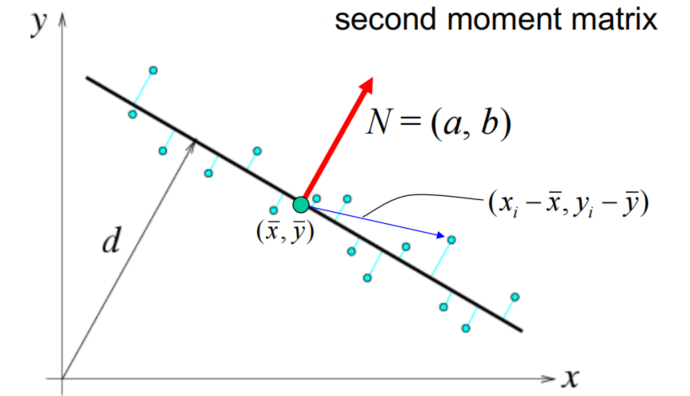
-
-> 为了减少离散点/outliers对最终拟合效果的影响,因此引入了以下两种方法
Robust Estimation 鲁棒性估计
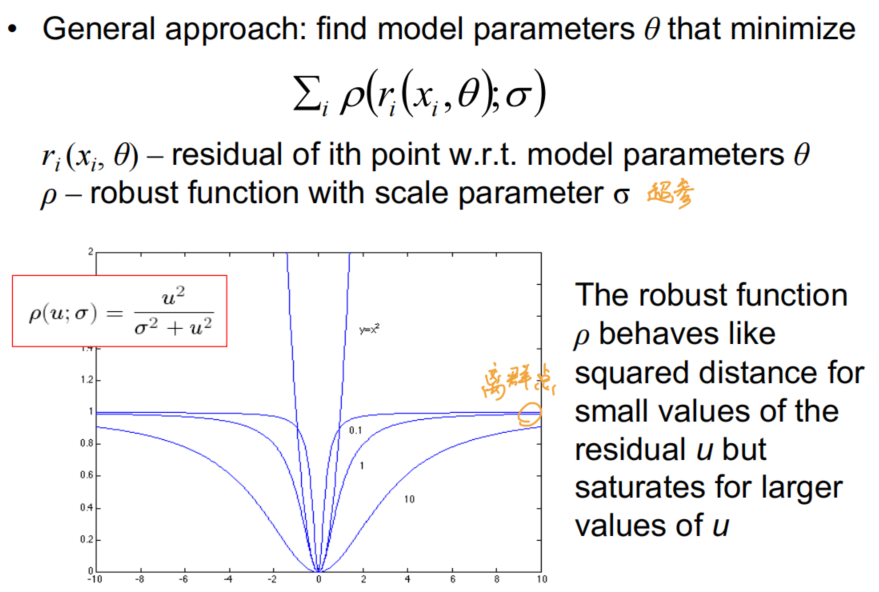
- 此方法是非线性优化问题,需要迭代进行,并且需要对超参数 进行选择来达到最优的效果
RANSAC 随机采样一致
- Overview:
- Choose a small subset of points uniformly at random
- Fit a model to that subset
- Find all remaining points that are “close” to the model and reject the rest as outliers
- Do this many times and choose the best model
- 需要对参数进行选择才能达到最优的效果:
- 初始的采样点个数
- 距离阈值
- 迭代的次数
-> 如果存在多条线
Hough Transform
- 引入霍夫参数空间(hough parameter space)和极坐标(polar system)的结合来进行表示
- 霍夫参数空间:
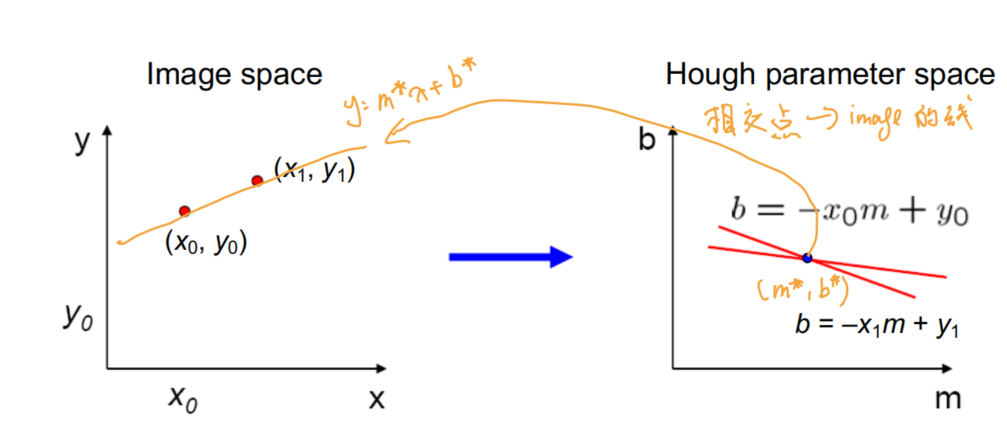
- 霍夫参数空间:
- 重复最多的点便是target参数的组合
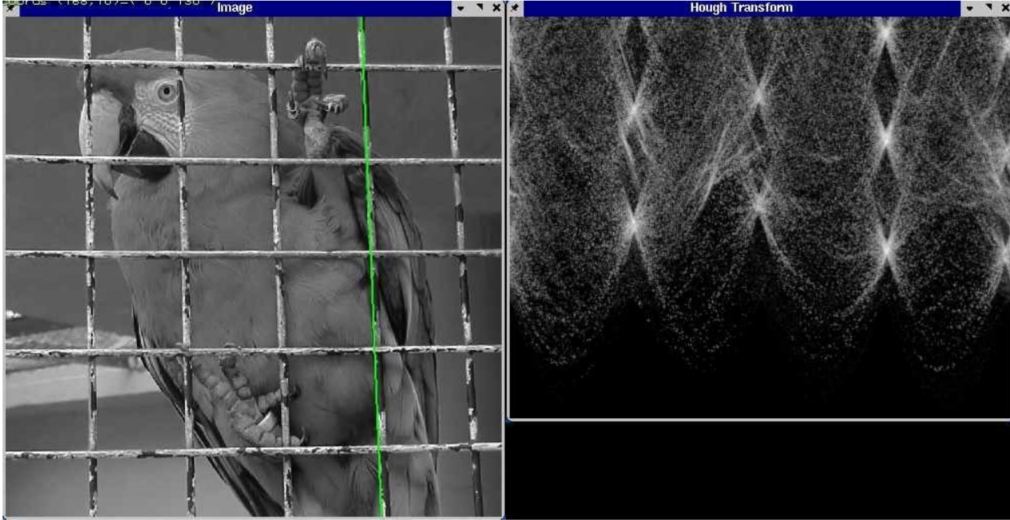
- 但该方法很容易受到noise的影响
- 选择一个好的网格/离散化
- 增加相邻的bins,使得累加数组更平滑
All articles in this blog are licensed under CC BY-NC-SA 4.0 unless stating additionally.










